0%
Binary Tree
1.Binary Tree Preoder, Inorder, Postorder traversal
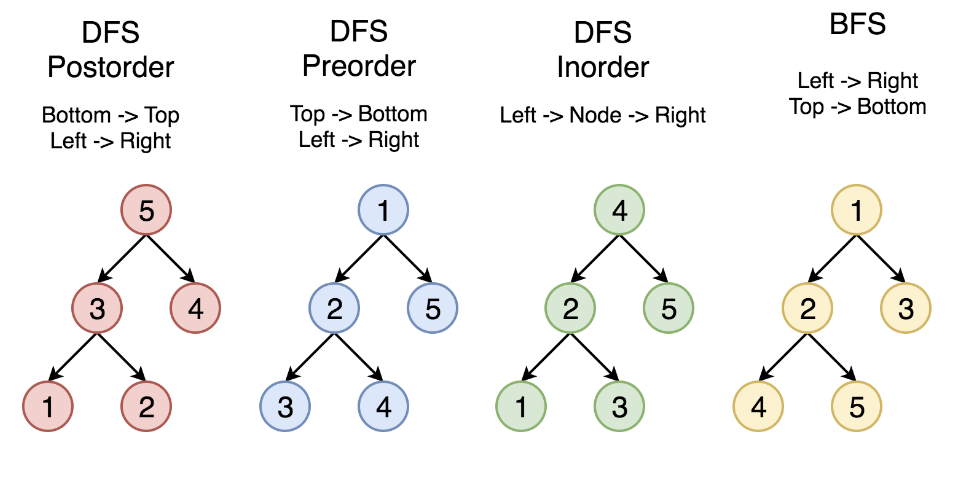
一套模版走天下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| class Solution {
根左右
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while(cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
res.add(cur.val);
cur = cur.left;
}
TreeNode temp = stack.pop();
cur = temp.right;
}
return res;
}
------------------------------------------------------------
左根右
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while(cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode temp = stack.pop();
res.add(temp.val);
cur = temp.right;
}
return res;
}
-------------------------------------------------------------
左右根 = 根右左 + 反过来存res
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while(cur != null || !stack.isEmpty()) {
while (cur != null) {
res.addFirst(cur.val);
stack.push(cur);
cur = cur.right;
}
TreeNode temp = stack.pop();
cur = temp.left;
}
return res;
}
}
|

